Find The Area Of A Circle With Circumference 32 Pi

As with triangles and rectangles, we can attempt to derive formulas for the area and "perimeter" of a circle. Calculating the circumference of a circle is not as easy as calculating the perimeter of a rectangle or triangle, however. In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century. That are not reused after they are calculated. This is in contrast to infinite series or iterative algorithms, which retain and use all intermediate digits until the final result is produced. The iterative algorithms were independently published in 1975–1976 by physicist Eugene Salamin and scientist Richard Brent.

These avoid reliance on infinite series. The approach was actually invented over 160 years earlier by Carl Friedrich Gauss, in what is now termed the arithmetic–geometric mean method or Gauss–Legendre algorithm. As modified by Salamin and Brent, it is also referred to as the Brent–Salamin algorithm. Second, since no transcendental number can be constructed with compass and straightedge, it is not possible to "square the circle".

In other words, it is impossible to construct, using compass and straightedge alone, a square whose area is exactly equal to the area of a given circle. Squaring a circle was one of the important geometry problems of the classical antiquity. Amateur mathematicians in modern times have sometimes attempted to square the circle and claim success—despite the fact that it is mathematically impossible. Its diameter is 57.28 feet the formula of circumference of circle is 2 pi r , from this calculate... (i.e. 7) than the number of digits needed to approximate it (i.e. 6).

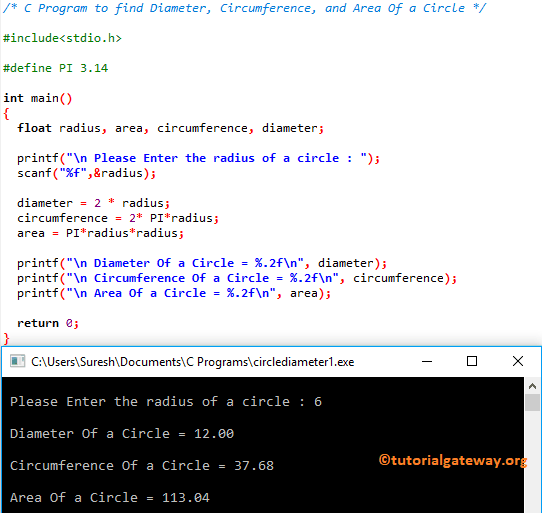
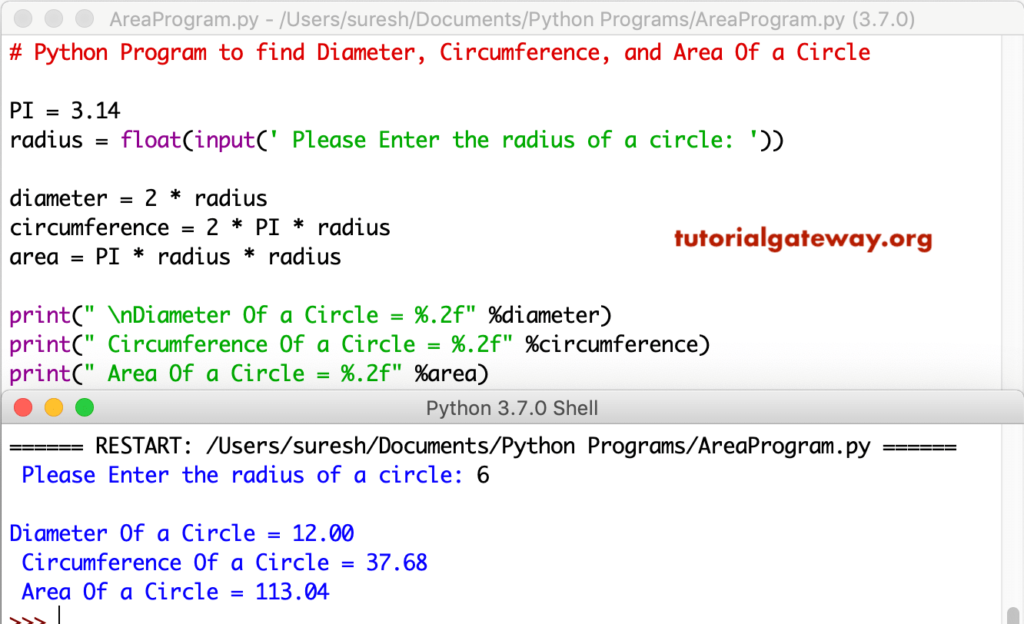
For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you. The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information. And to get the volume of a right circular cylinder, you take pi times the radius squared times the height.

Π is simply a ratio between the diameter, d of a circle and it's circumference. In other words, a circle that has a diameter of 1 or a radius of 1/2 will have a circumference of π. Π is conveniently also the ratio of r squared to the area of the circle, meaning that a circle with radius 1 will have an area of π. Let's take a look at some of your questions. The figure given below shows a kite, in which BCD is in the shape of a quadrant of circle of radius 42 cm.

ABCD is a square and ∆ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. By the way, this is one of those exercises that doesn't translate well into "real life". In reality, the sheet metal has thickness, and adjustments would be required in order to account for this thickness. Since the walls of a real-world tank have thickness, the real-world answer would not match the "ideal" mathematical one. There also exist non-circular smooth curves of constant width. Mathematicians John Wrench and Levi Smith reached 1,120 digits in 1949 using a desk calculator.

The primary motivation for these computations is as a test case to develop efficient algorithms to calculate numeric series, as well as the quest to break records. The extensive calculations involved have also been used to test supercomputers and high-precision multiplication algorithms. In the adjoining figure, ABC is a right angled triangle right angled at B. Semicircle are drawn on AB, BC and CA as diameter.

Show that the sum of areas of semi circles drawn on AB and BC as diameter is equal to the area of the semicircle drawn on CA as diameter. This line segment from the center to a point on the circle is called theradius. For example, the segment from P to F is a radius of circle 1. This line segment from the center to a point on the circle is called the radius. TachusPi by Fabrice Bellard is the program used by himself to compute world record number of digits of pi in 2009. M is the complexity of the multiplication algorithm employed.

Vega improved John Machin's formula from 1706 and his method is still mentioned today. Using fewer than five decimal digits in the numerator and denominator. Zu Chongzhi's results surpass the accuracy reached in Hellenistic mathematics, and would remain without improvement for close to a millennium. In 1630, a record only broken in 1699 when infinite series were used to reach 71 digits.

Circles show up all the time in the world around us so, naturally, being able to find the area of a circle is extremely useful in real life. For example, suppose you want to create a sandy beach area in your backyard in such a way that the beach is circular in shape. You need to figure out how much sand will be required and how much it's going to cost.

Following the discovery of the base-16 digit BBP formula and related formulas, similar formulas in other bases were investigated. Is made up of a large number of concentric circular pieces of very thin string. It is really easy to get overwhelmed when there is more than one variable involved. Sometimes your head feels like it is spinning when you see all of those variables.

Isn't math suppose to be about numbers? In other words, to get the surface area of a sphere, you take four times pi times the radius squared. And to get the volume of a sphere, you take the 4/3 of pi times the radius cubed. In other words, to get the area of a circle, you take pi times the radius squared. And to get the circumference of a circle, you take 2 times pi times the radius. The radius of a circle is decreasing at a constant rate of 0.1 centimeters per second.

In terms of the circumference C, what is the rate of the area of the circle, in square centimeters per second? The first person to calculate the Earth's circumference was Eratosthenes, a Greek mathematician, in 240 B.C. He discovered that objects in a city on the Northern Tropic do not throw a shadow at noon on the summer solstice, but they do in a more northerly location. Knowing this, and the distance between the locations, he succeeded in calculating the Earth's circumference. For simplicity, we'll use the former approach.

Thus, we can calculate the circumference of a circle if we know the circle's radius . For most calculations that require a decimal answer, estimating π as 3.14 is often sufficient. For instance, if a circle has a radius of 3 meters, then its circumference C is the following. The Circumference of a circle is the distance around the outside of it .

The circumference is equal to π times the twice the radius or the diameter . In the figure given below, the boundary of the shaded region in the given diagram consists of three semi circular arcs, the smaller being equal. If the diameter of the larger one is 10 cm, calculate. In the figure given below, ABCD is a square of side 14 cm and APD and BPC are semicircles.

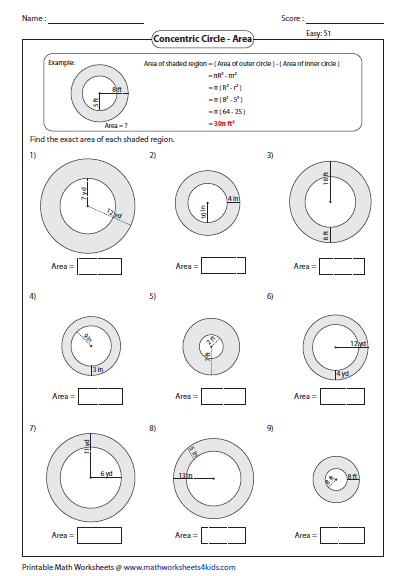
Find the area and the perimeter of the shaded region. Find the circumference of the circle whose area is equal to the sum of the areas of three circles with radius 2 cm, 3 cm and 6 cm. A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width.

Given that the area of the walk is 120 square metres, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x. Sometimes one value can be expressed as an expression of another value – these are called algebraic formulae. The line segment between two points on the circle and through the center is called thediameter.It is twice the length of the radius. For example, the segment from E to F is a diameter of circle 1. Notice how segment EF is twice as long as segment PF. This week your student will solve problems about the area inside circles.

We can cut a circle into wedges and rearrange the pieces without changing the area of the shape. The smaller we cut the wedges, the more the rearranged shape looks like a parallelogram. The line segment between two points on the circle and through the center is called the diameter.It is twice the length of the radius. This week your student will learn why circles are different from other shapes, such as triangles and squares. Circles are perfectly round because they are made up of all the points that are the same distance away from a center. A circular swimming pool with a diameter of 28 feet has a deck of uniform width built around it.

If the area of the deck is 60 square feet, find its width. Which critical thinking questions are necessary to ask when figuring out how trustworthy a piece of media is? (Select all correct answers.) Have my friends and family viewed... (F. C. M. Størmer).These approximations have so many digits that they are no longer of any practical use, except for testing new supercomputers. Properties like the potential normality of π will always depend on the infinite string of digits on the end, not on any finite computation. This interpretation implies a brim about 0.225 cubit (or, assuming an 18-inch "cubit", some 4 inches), or one and a third "handbreadths," thick (cf. NKJV and NKJV).

In March 2019, Emma Haruka Iwao, an employee at Google, computed 31.4 trillion digits of pi using y-cruncher and Google Cloud machines. Further progress was not made until the 15th century (through the efforts of Jamshīd al-Kāshī). The digits are large wooden characters attached to the dome-like ceiling. The digits were based on an 1874 calculation by English mathematician William Shanks, which included an error beginning at the 528th digit. The error was detected in 1946 and corrected in 1949.

Some of the formulae above are special cases of the volume of the n-dimensional ball and the surface area of its boundary, the (n−1)-dimensional sphere, given below. For similar formulas, see also the Ramanujan–Sato series. Is twice the smallest positive number at which the cosine function equals 0. The cosine can be defined independently of geometry as a power series, or as the solution of a differential equation.

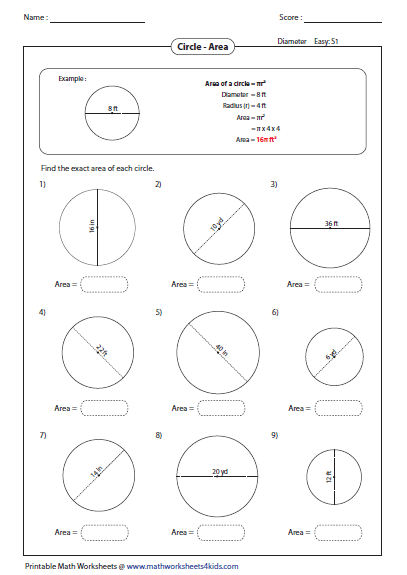
The area of a circle can be computed when given the circle's diameter. Learn how to find the area from diameter using the given formula and example solution, and discover applications of finding the area of a circle. The following function uses Math.PI to calculate the circumference of a circle with a passed radius. The best approach would be to write down the equations for the area of shaded region and then equate both sides. Your method worked because the final expression was written in the form where you could equate two expressions from LHS and RHS.

This may not be the case always and hence is not the best practice to follow. There are many formulas of of many types. Among others, these include series, products, geometric constructions, limits, special values, and pi iterations. If you know the diameter, simply divide by 2 to get the radius and use the same formula as above. If you know the diameter and not the radius, simply divide the diameter by 2 to get the radius and still use the formula above.

Quadrilateral wxyz has vertices w(-2,1), x(-1,3), y, and z(2,-1). Determine whether wxyz is a rectangle by using the distance formula and answering each question below. The circumference of a circle is pi times its diameter.

A figure consisting of a rectangle of length 8 cm and width 7 cm and two quarter-circles of radius 7 cm is cut from a piece of cardboard. Sometimes you need to do a little figuring. You may need to add, subtract, or take a fraction of the formula you came up with in step 2. For example, are you working with a circle, cylinder, square, etc?

Are you working with more than one figure? These are the questions you need to answer. And to get the volume of a rectangular solid, you take the length times the width times the height.

In this tutorial we will be solving problems using formulas to help us. We will be looking at such formulas as area of a rectangle, volume of a sphere, Pythagorean theorem and so on. After going through this tutorial, you will be an old pro at solving problems involving formulas. The rectangle shown has a perimeter of 108 cm and the given area. Its length is 6 more than five times its width. Write and solve a system of equations to find the dimensions of the rectangle.

Thus, a circle is simply the set of all points equidistant from a center point . The distance r from the center of the circle to the circle itself is called the radius; twice the radius is called the diameter. The radius and diameter are illustrated below. • We know that the area of a circle is π times the radius squared or ( 3.14 x r2). Use the this circle area calculator below to find the area of a circle given its diameter, or other parameters. To calculate the area, you just need to enter a positive numeric value in one of the 3 fields of the calculator.

You can also see at the bottom of the calculator, the step-by-step solution. Absolute Value - Example 2 In mathematics, the absolute value or modulus |x| of a real number x is its numerical value without regard to its sign. 4 is 4, and the absolute value of 4 is 4, both without regard to sign.

Absolute Value - Example 1 In mathematics, the absolute value or modulus |x| of a real number x is its numerical value without regard to its sign. A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube ? Also, find the ratio between the surface area of the original cube and the sum of the surface areas of the new cubes. A rectangular container, whose base is a square of side 6 cm, stands on a horizontal table and holds water upto 1 cm from the top.